Model Description
These physical models demonstrate basic principles underlying the behavior of thin-walled pressure vessels (TWPVs). Two models of TWPVs are used to explain forces inside of TWPVs. This demonstration should take 10-15 minutes.

Engineering Principle
The basic derivation for TWPV behavior (when ) states that for a cylindrical pressure vessel:
where the hoop stress is equal to the pressure times the inner radius divided by the wall thickness. The longitudinal stress is exactly half the hoop value. Therefore, a thin-walled pressure vessel is expected to fail due to hoop stress (failure plane along the length of the cylinder) long before it will fail due to longitudinal stress.
What You Need
| Item | Quantity | Description/Clarification |
|---|---|---|
| Wooden Model | 1 | A wooden cylinder about 3” in diameter and 6” long. The cylinder is cut in half along the longitudinal axis. Pegs are put through one half and holes are drilled into the other so that the two halves can be put together and taken apart easily. |
| Plastic Model | 1 | Cylinder is hollow and made of four pieces. The cylinder is approximately 12” long and 4½” in diameter. It is cut in half twice, once along the longitudinal axis and once through the cross-section. The four pieces fit together with pegs that protrude from the side of each piece. The top and bottom of the cylinder are made of clear plastic and screwed onto the opaque sides (grey in this case). |
| White Pen or Marker | 1 | The wooden model has the planes and stresses drawn on it with white pen to better demonstrate how stresses flow through a cylinder. |
How It’s Done
Before Class: Paint the wooden model black and draw the forces and label the planes with the white pen or marker. Make sure the two models are easily taken apart and put back together so there are no issues during class.

In Class: Show the students the two models and ask: how is the internal cylinder pressure carried by the cylinder? Use the two models to show/explain the two different kinds of stress: hoop and longitudinal. Hoop stress is applied around the circumference, while longitudinal stress is applied along the length of the cylinder. The wooden model shows the two planes in which the internal stress act. The hoop stress is applied on the transverse plane (figure below, left), while the longitudinal stress is applied on the longitudinal plane (figure below, right). This physical model physically represents the planes the internal pressure acts upon.

Using the plastic model, show how a TWPV can fail due to these two stresses. When a vessel fails due to longitudinal stress, it fails along a circumferential plane.

When a vessel fails due to hoop stress, it fails along a longitudinal plane.

Additional Application: Derive the formulas for TWPVs directly from the plastic cylindrical model using only a section of the cylinder.
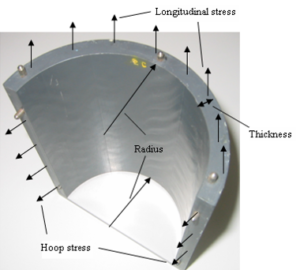
Using the model, help the students visualize how the internal pressure acts on the cylinder and generates internal stresses in the cylinder walls. Pull from the students that there are both internal stresses acting in the longitudinal and circumferential directions.
To solve for the longitudinal stress, we use an equation of equilibrium for the forces due to generated internal cylinder stress and the force due to internal pressure. Those forces are best seen when the cylinder is cut perpendicular to the longitudinal axis exposing the circular hollow cross section of the cylinder and the circular area of the pressurized fluid in the cylinder. The force due to the resulting longitudinal stress is equal to the stress multiplied by the area of the wall of the vessel around the circumference. The force due to internal pressure is equal to the pressure multiplied by the area of the fluid plane exposed by the cross-sectional cut of the cylinder.
To solve for hoop stress, we use an equation of equilibrium for the forces due to generated internal cylinder stress and the forces due to internal pressure. Those forces are best seen when the cylinder is cut parallel to the longitudinal axis exposing the oblong hollow cross section of the cylinder and the oblong area of the pressurized fluid in the cylinder. The force due to hoop stress is equal to the stress multiplied by the exposed area of the wall of the cylinder along each side of the cylinder. The force due to internal pressure in that plane is equal to the pressure multiplied by the area of the fluid plane exposed inside by the longitudinal cut of the cylinder.
Both of these cuts and the exposed internal cylindrical stress are seen above. From these equations, we determine that the hoop stress is two times as great as longitudinal stress, thus a thin-walled pressure vessel would normally fail due to hoop stress before longitudinal stress.
